EMPIRICAL PREDICTION OF THE GLOBAL TEMPERATURE ANOMALY FOR 2003

 

Chris Folland & Andrew Colman

 

UK DEPARTMENT OF THE ENVIRONMENT, TRANSPORT AND THE REGIONS

 

1.    INTRODUCTION

 

Global temperature is an important indicator of global climate, and has been at or near record levels in recent years. Analysis of observed and model data has linked interannual to decadal fluctuations in global mean temperature to various natural phenomena including ENSO, volcanic activity and solar flux variability. Global temperature change in recent decades has also been firmly linked to human activity, including changing greenhouse gas and aerosol concentrations and stratospheric ozone depletion and tropospheric ozone increases.  The existence of these numerous forcings raises the possibility of skilful predictions of global temperature.  In this study, indices of the known important climate  forcings and influencing phenomena are used to make empirical predictions of the global temperature anomaly from a 1961-90 average. Based on a multiple regression analysis, the state of ENSO is the most important predictor on the interannual time scale.  On the multi-decadal time scale the net  radiative forcing of the atmosphere is most important.

 

We use two forms of multiple linear regression to make these forecasts (a) using predictors based on physical understanding which are forced into the regression (b) a modified version where one of the predictors is a forecast of SST anomaly in the Nino3.4 region of the Tropical Pacific. The latter was chosen to be the forecast made by the US National Center for Environmental Prediction (NCEP) coupled ocean-atmosphere global circulation model. This model was chosen, as it is possible to assess the intrinsic skill of the method from published hindcasts and previous forecasts.

 

1.1  PREDICTORS

 

The six predictors listed below have been identified by more than one author to be related to large-scale temperature:

 

a)       ATHC: Atlantic ThermoHaline Circulation index. This is an  index  of mean North Atlantic SST with the global change component (represented by the first EOF of Low pass filtered  global SST) removed.  It is considered to be a better index of thermohaline circulation than the Inter- Hemispheric Contrast  ( IHC) index it replaces. Recent work by Knight et al (2003) seems to confirm that the value of this index should affect global mean temperature.

b)       ENSO HF1: The High Frequency El Nino Southern Oscillation index 1 (ENSO HF 1). This is the time series of the first covariance eigenvector of high frequency (<13 years) global SSTA for 1911-95 in Folland et al (1999). This eigenvector pattern is related strongly to ENSO.

c)       ENSO HF2: The High Frequency El Nino Southern Oscillation index 2 (ENSO HF 2). This is the time series of the second covariance eigenvector of high frequency (<13 years) global SST. This eigenvector pattern is also ENSO-related, but the time series is 6-9 months out of phase with HF ENSO 1. This pattern is also from Folland et al (1999).

d)       VOLCANO: An index of global volcanic dust cover (VOLCANO) produced by Sato et al (1993). Dust veils from major volcanic eruptions, particularly in the tropics, lead to a significant drop in global temperature for a year or two after the eruption.

e)       SOLAR: An index of solar irradiance (SOLAR) as supplied by Lean (Frohlich & Lean, 1998) and extrapolated to the present.

f)        GSO: An estimate of the global mean anthropogenic net radiative forcing at the tropopause. This comes from changing concentrations of well-mixed anthropogenic greenhouse gases, the direct and indirect effects of sulphate aerosol emissions and from stratospheric and tropospheric ozone concentration changes (GSO).  This index was calculated using the Hadley Centre’s current Coupled Ocean-Atmosphere general circulation model, HaDCM3. It is expressed as the annual mean forcing at the top of the troposphere in wm-2  (Johns, personal communication).

g)       NCEP NINO 4: In  one  forecast, predictions of the Nino3.4 area (170-120oW, 5oN-5oS) SST anomaly made by the NCEP coupled ocean-atmosphere global circulation model  (NCEP NINO3.4) are used.  This replaces ENSO HF1 in the previous equation, and no ENSO HF2 index is  used.

 

The North Atlantic Oscillation does not contribute significantly in the regression method probably in part because there are large areas of negative as well as positive anomalies. In addition there is a large amount of interannual variability, so predictions one year ahead based on its value in previous years may have little predictive skill. Similarly the Interdecadal Pacific Oscillation or the similar Pacific Decadal Oscillation does not contribute, probably because it is highly correlated with ENSO. Future work will investigate this in more detail as small residual effects on global temperature may exist.    

 

We chose 1947-2001 as our training period because the predictor and predictand data are best at that time. Soon,  advances in historical data sets might allow this period to be substantially extended. In the cross validation skill testing method, we allow for serial correlation on the interannual time scale as described below. The multiple regression equations include December data of the prior year

 

Predictor data for the following periods are used. The examples are for the 2003 prediction.

 

ATHC                    January-December  2002

ENSO HF1            October-December 2002

ENSO HF2            October-December  2002

VOLCANO           December 2002 (extrapolated from data ending in 1997 assuming no significant recent activity)

SOLAR                  January-December  2002 (Extrapolated from data up to 1998 by Lean allowing for the solar cycle

                               (pers. comm.)

GSO                       January-December  2002

NCEP NINO3.4     January-June  2003 forecast (used in place of ENSO HF1 )

 

Note: December 2002 SSTA are based only on observations from 2nd-11th December. In real-time forecasts this data is effectively persisted for the whole month, whereas in the training data the whole month is used.

 

The predictor periods chosen were selected to extract maximum available skill from data available at the time of the forecast. Updating to December is only influential for SSTA based predictors.  So far, no investigation of the optimum  lags have been made  concerning the radiative forcing data predictors, which are based on the prior year but we believe the method to be rather insensitive to such choices.

 

1.2 PREDICTAND

 

The predictand  is mean global land surface air and sea surface temperature anomalies relative to 1961-90 for the forthcoming year. This is chosen to be the IPCC Third Assessment Report optimally averaged series produced by the Hadley Centre and the Climatic Research Unit (Folland et al, 2001). Optimum averaging objectively allows for data gaps as well as observational uncertainties. The changes in annual global mean temperature anomalies for recent years are, however, small. Note that the global mean temperature estimates for 2001 and 2002 are not optimally averaged.

 

1.3 FORECAST METHOD

 

Three forecasts are made using multiple linear regression (METHODS 1-2). A global temperature anomaly forecast is produced by applying each regression equation to the  predictor indices described above. All regression equations use historical data for 1947-2001. The two regression equations are:

 

1.        An equation using predictors a-f of section 1.1,  calculated using data for 1947-2001.

2.    A modified method using NCEP couple model forecasts of  the NINO3.4 SSTA index for January-June  of 2003 instead of observations of  HF ENSO EOF 1 for late 2002.  The NCEP forecast is corrected for bias compared to observations estimated from 18 model hindcasts from 1982-2000

 

The forecast from each model is modified to use "inflated" linear regression to retain the same forecast variance as observed variance. However because of the high correlation skill of these methods, the level of inflation is small. The Forecast Probability Distribution Function (FPDF) for each method is based on the assessed standard errors of the regression predictions, assuming the forecast errors are normally distributed. 

 

A third forecast model using an orthogonalised version of predictors a-f  in section 1.1 was dropped this time as forecasts from the orthogonal predictors are very highly correlated with model 1 and hence were not considered to provide useful extra information.

 

1.4 ASSESSMENT METHODS

 

To estimate forecast skill, trial forecasts (hindcasts) were made using the "jack-knife" method in a fairly severe way. Jack-knife forecasts were made for every year in the data period used to create the forecast equations using equations calculated using the majority of the remaining years in that period. Thus the coefficients of the predictors change from year to year but the predictors do not. The forecast year is always excluded from the regression equation, along with data for the 5 years before and 5 years after the forecast year. During the first and last five years of the data period only a one sided exclusion of data is possible. This "jack-knife" process minimises artificial hindcast skill due to persistence.

 

In real time forecasts, we only have an estimate of December SST up to about December 11th . Two measures of forecast skill are used:

 

(a)     Correlation: Standard (Pearson) Correlation. This ignores biases between forecast and observed values and the difference in standard deviation between the forecast and the observed value. We use a total correlation score (correlation) and a high frequency correlation (HF correlation). The latter calculates correlations on time scales less than about 10 years and is essentially a measure of the interannual skill.

(b)     RMS (Root Mean Square error):  RMS scores are very appropriate  as the forecast standard deviation is equal to that observed. 

 

 

2.       PERFORMANCE OF HINDCASTS AND  FORECASTS  OF OPTIMALLY AVERAGED GLOBAL TEMPERATURE ESTIMATES

 

2.1 JACK-KNIFE HINDCAST  SKILL 1947-2001

 

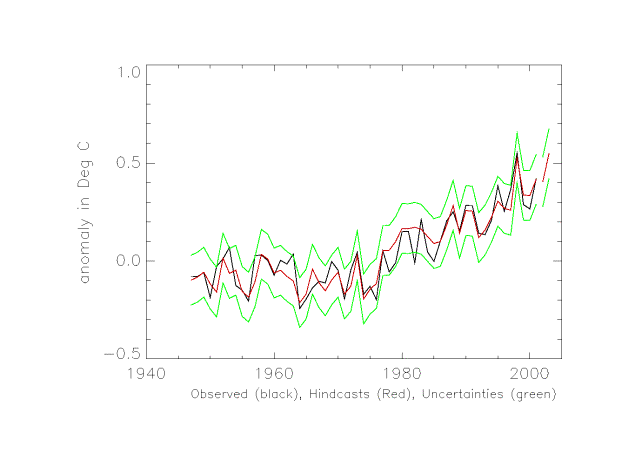
Jack-knife multiple regression forecasts are plotted against observed global temperatures in figure 1 for METHOD 1. The jack-knife correlation of 0.93 is very high for a climate prediction scheme. Because an important aim of the forecasts is to indicate how next year will differ from this year, the high frequency correlation of 0.74 gives a more realistic estimate of skill on this time scale. Nevertheless the excellent reconstruction of the low frequency variation of global temperature would only be possible  if the shape of the low frequency forcing had been captured well and this forcing explained much of global temperature on multi-decadal time timescales. So our technique to some extent corroborates current estimates of the time-dependent shape of the total net radiative forcing. However, as long as the shape of such forcing is well captured, our method would not be sensitive to the overall magnitude of radiative forcing change. In Figure 1, 40% and 95% confidence intervals are plotted in green and the best estimate forecasts in red. 

 

Table 1 shows the contributions of the different predictors in METHOD1. The regression equation is built up in a stepwise manner, with predictors incorporated in order using the results of an F test. The importance of each predictor is shown by the standardised regression coefficient. This is the coefficient estimated when both predictor and predictand index are standardised.   Bold numbers show the skill of the complete regression equation.


 

TABLE 1 PERFORMANCE OF JACK-KNIFE HINDCASTS 1947-2001 ADDING 1 PREDICTOR AT A TIME,

USING SIX PREDICTORS  (METHOD 1)  

 

 

Predictor added

Standardised

Coefficient

(1947-2001)

Correlation

1947-2001

HF Corr.

1947-2001

RMS

1947-01

     oC

RMS

Stand. Units

GSO

0.82

0.83

0.29

0.109

0.609

ENSO HF 1

0.38

0.85

0.62

0.099

0.553

VOLCANO

-0.24

0.89

0.70

0.083

0.462

SOLAR  

0.14

0.90

0.71

0.079

0.439

ATHC

0.16

0.93

0.70

0.068

0.379

ENSO HF 2

-0.11

0.93

0.74

0.065

0.362

 

 

The strongest predictor (over 1947-2001), the GSO index , predicts the warming trend this century and the accelerated warming over the past 30 years but does not predict variability on time scales much less than 20 years.  The second predictor,  ENSO HF 1, contributes most to interannual skill. The third predictor, VOLCANO, is important only during the 2 or 3 years following a major eruption. It is zero in the 2003 forecast.                      

 

TABLE 2  SUMMARY PERFORMANCE OF JACKKNIFE FORECASTS USING ORTHOGONAL PREDICTORS AND USING NCEP NINO3.4 SST FORECASTS AS A PREDICTOR.

 

Predictors

Assessment

Period

Correlation

 

HF Corr.

 

RMS

     oC

RMS

S. U.

Method 1

1947-2001

0.93

0.74

0.065

0.362

Method 2 (ENSO represented by

NCEP NINO 3.4)

1982-2001

0.83

0.73    

0.078

0.436

 

The method using NCEP Nino3.4 forecasts has somewhat less correlation skill than method 1 but comparable HF correlation skill. However, these assessments are substantially less reliable than those due of Method 1 due to the short period of testing.   

 

 

2.2 ASSESSMENT OF FORECAST FOR 2002 

 

The forecasts for 2002  were expressed as the boundaries corresponding to the following values of the cumulative probability of the forecast, starting at the coldest level:

 

 

 

 

2.5%

30%

50%

70%

97.5%

Method 1

0.31

 

0.39

 

0.44

 

0.48

 

0.57

 

Method 2

0.36

 

0.46

0.52

 

0.57

 

0.68

 

Weighted Mean

0.33

0.42

0.47

0.52

0.61

 

 

 


The mean forecast anomaly of 0.47oC was based on a skill-weighted average of the two methods using overall correlation. The observed anomaly  to October for both land surface air temperature and SST, and for November and early December SST only is  assessed to be  0.49oC. So the 2002 forecast may have been slightly cooler than observed but was within about the 25% confidence range of the forecasts. Hence the 2002 forecast can be considered an ACCURATE forecast. At present, we are also correct in predicting  2002 to be the 2nd  warmest year on record.

 

2.        FORECAST FOR 2003 

 

The best estimate forecasts of global temperature anomaly made by the two methods were:

 

1.        USING SIX EMPIRICAL PREDICTORS INCLUDING OBSERVED ENSO INDEX, OCT-DEC 2002   0.55 oC

 

2.        AS 1 BUT USING NCEP NINO3.4 SST  FORECAST FOR JANUARY-JUNE 2003                                 0.55 oC

 

The associated probability forecasts are expressed as the boundaries corresponding to the following values of the cumulative probability of the forecast, starting at the coldest level. The mean and standard deviation is calculated by  weighting the forecasts according to their intrinsic skill as measured by total variance explained in the cross validated tests.  

 

 

2.5%

25%

50%

75%

97.5%

Method 1

0.42

0.51

0.55

0.59

0.68

Method 2

0.39

 

0.50

0.55

 

0.60

 

0.70

Weighted Mean

0.41

0.50

0.55

0.60

0.69

 

 

Our best estimate forecast of the global temperature anomaly for 2003 is 0.55+-0.14oC, with a 95% confidence range from 0.41oC  to 0.69 oC.  The best estimate forecast  is for a year equal in temperature to the warmest year on record (1998, 0.55oC). There is  thus a 50% probability that 2003 will be as warm, or warmer than the warmest year, 1998 but only a 20% probability that 2003 will be as cool or cooler than 2002, the second warmest year, provisionally assessed to have an anomaly of 0.49oC.

 

References:

 

Folland, C.K  & Colman, A.W., 2001: Empirical Prediction of the global temperature anomaly for 2001. Experimental Long Lead Forecast Bulletin 9 4 published by COLA, USA, www.iges.org/ellfb

 

Folland, C.K  & Colman, A.W. 2000: Empirical Prediction of the global temperature anomaly for 2000. Experimental Long Lead Forecast Bulletin 9 1 published by COLA, USA, www.iges.org/ellfb

 

Folland, C.K., Parker D.E., Colman AW. and R. Washington, 1999: Large scale modes of ocean surface temperature since the late nineteenth century. Chapter 4, pp73-102 of Beyond El Nino: Decadal and Interdecadal Climate Variability.  Ed: A. Navarra.  Springer-Verlag, Berlin, pp 374.

Folland, C.K., Rayner, N.A., Brown, S.J. Smith, T.M. Shen, S.S. Parker, D.E., Macadam, I., Jones, P.D., Jones, R.N., Nicholls, N. and Sexton, D.M.H., 2001: Global temperature change and its uncertainties since 1861. Geophys. Res. Lett., 106, 2621-2624.

Frohlich,  C. and Lean, J. 1998: The sun's total irradiance: cycles, trends and related climate change uncertainties since 1976.  Geophysical Res. Lett., 25, pp 4377-4380.

Knight, J., Allan R.J., Folland, C.K., and M. Vellinga, 2002: Variations in the thermohaline circulation and climate. Submitted to Science.

 

Jones, P.D., 1994: Hemispheric surface air temperature variations: a reanalysis and an update to 1993, J. Climate, 7:1794-1802.

Parker, D.E., C.K. Folland, and M. Jackson, 1995: Marine surface temperature: observed variations and data requirements, Climatic Change, 31:559-600.

 

Sato, M., J.E. Hansen, M.P. McCormick and J.B. Pollack, 1993: Stratospheric aerosol optical depths, 1850-1990. J. Geophys. Res., 98, 22987-22994.


Figure 1: Jack-knife hindcasts of optimally averaged global mean temperature anomalies for 1947-2001 (red line to 2001) and forecasts for 2002 and 2003 (short red line) using method 1. The black line represents observations based on optimal averages. The  95% confidence interval is marked by lines in green.